A graph is planar if it can be drawn in a plane (two dimensions, ie on a piece of paper) without graph edges crossing.
A subdivision of a graph G=(V,E) is a graph resulting from taking an edge e in E with endpoints u,v in V, introducing a new vertex w, and replacing e with two new edges, one between u,w and one between w,v.
Kuratowski's Theorem states that a graph with a finite number of vertices V and edges E is planar if and only if it does not contain a subgraph that is a subdivision of (1) the completely connected graph on five vertices or (2) the complete bipartite graph on six vertices, three in each partition.
Completely connected graph on five vertices:
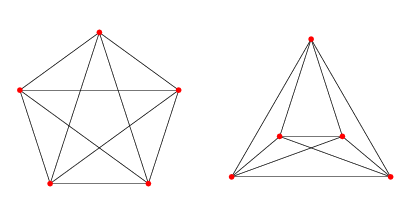
Image from mathworld.
Complete bipartite graph on six vertices with 3 in each partition:
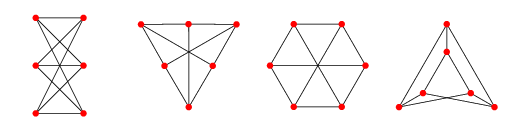
Image from mathworld.